티스토리 뷰
이번 IOI에 한국 국가대표로 선발이 되어서, 본 대회를 치르게 되었습니다. 코로나19가 계속되는 바람에 올해도 싱가포르 현지에서 대회를 치르지 못하고 우리나라에서 온라인으로 치르게 된 점이 아쉽습니다.
작년에 이어 2년째 IOI에 참가하게 되었는데, 작년과는 느낌이 확연히 다른 대회였습니다. 작년과 다르게 올해는 주변 누구도 성적에 대한 기대를 가지지 않아서 편한 마음으로 시험을 볼 수 있었습니다. 아마 이러한 점도 성적에 영향을 주지 않았나 싶습니다.
Day 0 (Practice Session)
연습 세션 문제는 작년과 거의 똑같았습니다. 차이점이 있다면, 무슨 이상한 전처리를 해야 맞는 문제 하나가 간단한 bfs 문제로 바뀌었습니다. 작년에 끝까지 풀지 못했던 문제(Jelly Flavours)를 이번에는 쉽게 풀어내서 기분이 좋았습니다...만, 예전에 풀이를 들어서 은연중에 기억에 남아 있었다는 사실은 감안해야 할 것 같습니다.
Day 1
시작 ~ 6분 (3 0 0)
처음부터 욕심 부리지 말고 차근차근 서브태스크만 긁어야겠다는 생각이 들어서, 일단 문제를 빠르게 읽었습니다. 문제에서 느낀 첫인상은 이랬습니다.
- A(Candies)는 전형적인 수열과 쿼리 느낌이었는데, 문제의 생김새를 보니 세그먼트 트리 비츠를 써야 할 것 같다는 느낌이 들었습니다. 한편 서브태스크 중에 $l=0, r=n-1$인 서브태스크가 있는데, 루트질을 시도해볼 수 있겠다는 생각을 했습니다.
- B(Keys)는 어려운 그래프 문제 같다는 생각이 들었습니다. 37점까지는 단순 나이브가 돌 것이고, 그 이상 점수를 얻기 위해서는 의미 있는 관찰 여러 개를 해야 할 것 같았습니다.
- C(Fountain Parks)는 부분점수를 얻기 가장 쉬워 보였고, 서브태스크 배점도 가장 단순했기 때문에, 세 문제 중 가장 쉬울 것으로 추측했습니다. IOI에서 나온 문제 치고는 특이하다는 생각이 들었습니다.
이후 아무 생각 없이 A에서 3점을 긁고, 다음 문제로 향했습니다. 3점 서브태스크는 $O(NQ)$ 시뮬레이션으로 풀 수 있었습니다.
~ 39분 (3 0 5)
C가 가장 쉬울 것이라고 추측해서 C를 무조건 풀어야겠다고 생각했습니다. 작년같은 경우는 Day 1, Day 2 모두 쉬운 문제가 하나씩 있었기 때문에 이번에도 주는 문제가 하나쯤 있지 않을까 생각하고 C를 시도했습니다. 그러나 짧은 시간 안에 생각할 수 있는 construction은 모두 반례가 있었고, 오랜 시간 큰 소득이 없어서 그냥 5점 서브태스크만 긁고 런했습니다.
5점 서브태스크는 $x_i = 2$인 서브태스크로, 모든 분수를 $y$좌표 순으로 정렬하고 나면 쉽게 풀 수 있습니다.
~ 56분 (3 37 5)
아직 긁지 않은 문제가 B밖에 없었기 때문에, 간단하게 B 37점을 긁었습니다. 슬슬 뭔가 말리고 있다는 생각이 들었습니다.
37점 서브태스크는 단순한 시뮬레이션으로 풀립니다. 시작 정점을 잡고, 열쇠를 추가해 가면서 지나갈 수 있는 간선을 하나씩 보면 됩니다. 다만 이걸 단순히 하면 $O(N^2 M)$ 근처 시간이 걸릴 것이고, 조금 머리를 쓰며 시뮬레이션을 하면 $O(NM)$으로 줄일 수 있습니다.
~1시간 12분 (38 37 5)
다시 수쿼로 돌아가 보았습니다. 서브태스크를 차분히 읽어보니 2번 서브태스크(8점)도 쉬웠습니다. 사탕의 수가 계속 증가하기 때문에, 일단 $c_i$를 고려하지 않고 계속 추가해준 뒤 마지막에 $c_i$를 고려해 주면 됩니다. 8점 서브태스크를 빠르게 긁었습니다.
다음으로 모든 $c_i$가 같은 27점 서브태스크를 고민해 보았습니다. 쿼리를 루트 개씩 쪼개면 각각의 쿼리 집합에서 등장하는 $l_i$와 $r_i$는 최대 $2 \sqrt{Q}$개이기 때문에 같은 종류의 쿼리에만 영향을 받는 구간을 고려해줄 수 있습니다. 따라서 문제를 모든 쿼리가 $l=0, r=n-1$인 경우로 환원할 수 있습니다. (추후 블로그 포스팅 예정)
이제 모든 가방의 용량이 $cap$로 고정되었을 때, 가방에 담긴 사탕의 수가 쿼리들에 의해 어떻게 영향을 받는지 분석해 봅시다. 총 $Q$개 쿼리에 대해 분석할 것인데, 이때 처음에 $x$만큼 사탕이 담긴 가방에서 $i$번 쿼리까지 처리한 이후 사탕의 양을 $f_i (x)$라고 합시다. $f_0(x)=x$이 성립하며, 우리가 구하고자 하는 함수는 $f_Q(x)$입니다.
$f(x)$에 여러 가지 조작을 해 보면 함수가 항상 아래와 같은 형태라는 것을 알 수 있습니다.
$$
f(x) = \cases{ A+C, & $(x \le A)$ \\
x+C, & $(A \le x \le B)$ \\
B+C, & $(B \le x)$
}
$$
따라서 세 변수 $A, B, C$를 쿼리를 지날 때마다 적당히 조절해줄 수 있습니다. 초기에 $A=0$, $B=cap$, $C=0$입니다. 이렇게 $A, B, C$를 계산하고 나서 최종 답을 구할 때에는 단순히 $f_Q(x)$를 구해 주면 됩니다.
이때 예외가 존재합니다. 처리하는 도중에 $A > B$가 되어버릴 수 있습니다. 이러한 상황이 발생하는 경우, 최종 상태가 초기 상태에 영향을 받지 않는다는 뜻이므로 초기에 0이었다고 가정하고 naive하게 계산해 줘도 무방합니다. 이때 시간 복잡도는 $O((N+Q) \sqrt Q)$로 서브태스크 3을 해결할 수 있습니다.
위 풀이를 구현하였고, A에서 점수가 38점이 되었습니다.
~ 1시간 34분 (38 37 55)
B에 대해서도 약간 생각해 봤지만, 별로 진전이 없었고 C에서 부분점수를 긁기로 했습니다. C에서 네 점이 $2 \times 2$ 사각형을 이루지 않는 경우 재미있는 construction이 가능합니다.
- 분수 중 $x+y \equiv 0 \ (\mod 4)$인 것에 색칠을 합니다.
- 거리가 2인 인접한 모든 분수 사이를 연결합니다.
- 모든 연결된 분수 쌍에는 정확히 하나의 색칠된 분수가 존재하는데, 이때 색칠된 분수의 위치에 따라 아래 그림과 같이 벤치를 배치합니다. (아래 그림에서 검은색 원이 색칠된 분수입니다.)
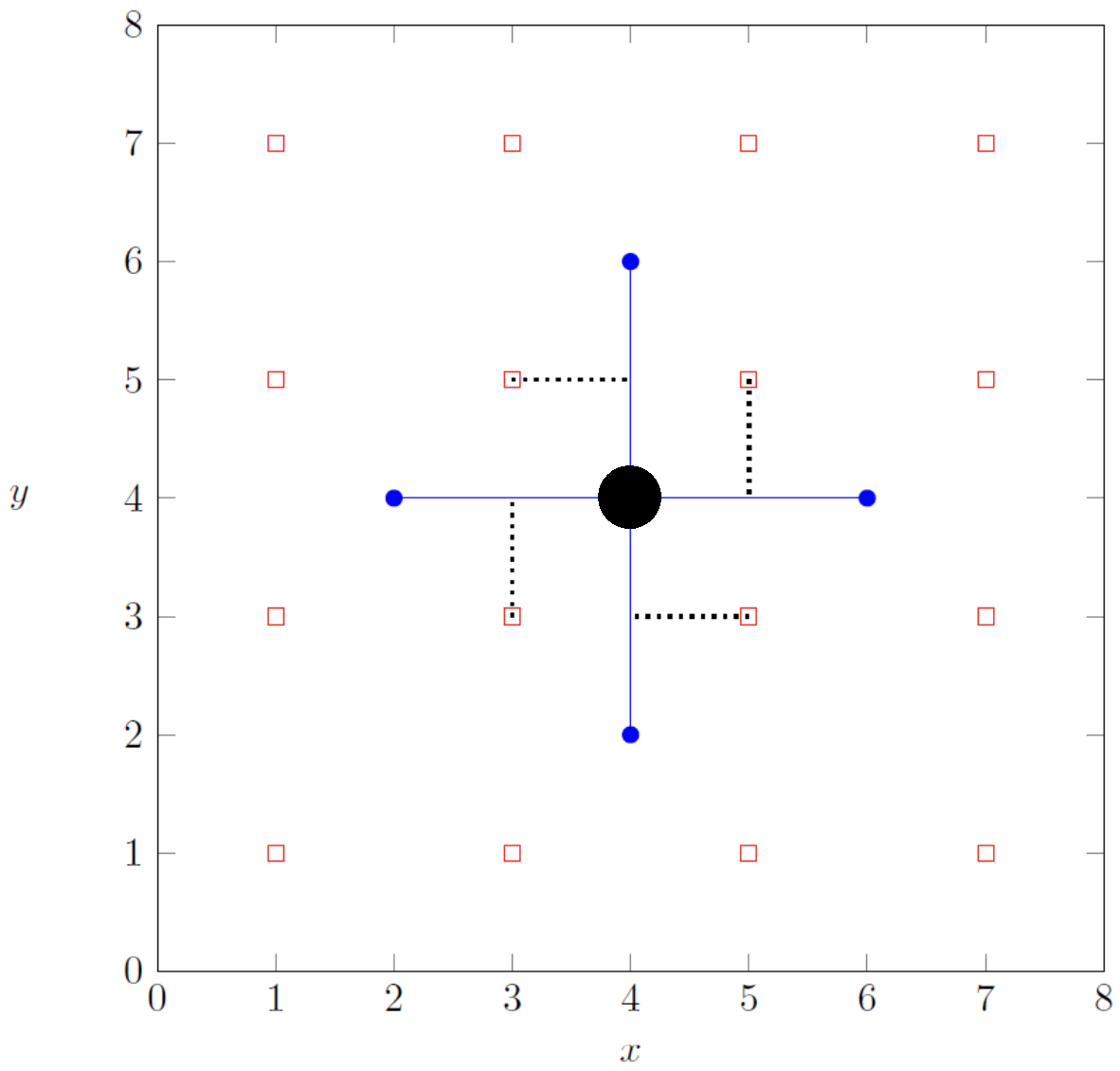
왜 이러한 construction이 성립할까요? 어떤 벤치가 두 개 이상의 경로에 의해 벤치로 선정되려면, 그 주변 네 개의 짝수점 모두에 분수가 있어야 하기 때문입니다. 이러한 경우가 존재하지 않는 서브태스크 4와 5를 맞을 수 있습니다.
서브태스크 2는 다른 방법으로 풀리지만, 여전히 쉽습니다. 앞과 같이 모든 분수 사이를 이은 다음에, 세로 선분은 $x=2$인 경우 왼쪽 벤치와, $x=4$인 경우 오른쪽 벤치와 연결하고, 가로 선분은 아래 벤치와 연결하면 됩니다.
여기까지 긁어서 C 점수가 55점이 되었고, 총점은 130점이 되었습니다.
~ 3시간 22분 (38 37 55)
이후 한동안 진전이 없었습니다. A는 뭔가 세그먼트 트리 비츠가 필요해 보여서 반쯤 포기한 상태였고, B는 SCC를 쓰면 어떻게든 될 것 같아서 구현해봤지만 코사라주 알고리즘에서 계속 구현 미스를 내서 틀렸고 심지어 풀이가 맞는지도 확신이 없던 상황이었습니다. C는 55점 풀이를 기반으로 랜덤을 추가해 어떻게든 뚫어 보려고 시도했지만 잘 되지 않았습니다.
~ 3시간 35분 (38 37 70)
아무리 봐도 망한 상황이었지만, 일단 마음을 다잡고 뭐라도 긁어 보려 했습니다. C의 $2 \le x \le 6$인 섭테를 긁어 보려 했는데, 어떻게든 하면 풀 수 있었을 것 같았지만 케이스워크가 무시무시해서 별로 짜고 싶지 않았습니다. 그래서 랜덤 풀이를 계속 발전시켜 DFS를 BFS로 바꾸고, 시작점을 이곳저곳으로 바꾸고, 해가 안 나오면 될 때까지 랜덤하게 돌리고... 이렇게 하다 보니 3번 섭테가 뚫렸습니다. 이 시점에서 C에서 더 이상 점수를 받아야겠다는 생각을 완전히 버렸습니다.
~ 3시간 59분 (38 67 70)
이후 코사라주의 올바른 구현이 떠올라서(...) 수정해 봤으나 이제는 TLE가 났고, SCC 돌리는 횟수를 30회에서 15회로 줄였더니 67점 섭테가 긁혔습니다. 이 풀이는 틀린 풀이로 반례가 존재하므로 따로 설명하지 않겠습니다.
~ 4시간 17분 (67 67 70)
어느 정도 멘탈을 되찾은 것 같았지만 아직도 작년 Day 1보다 점수가 낮았습니다. 물론 작년보단 어려운 것 같았지만 이대로 가면 금메달은 불가능하다고 생각했고(알고보니 정확히 금 컷이긴 했지만...) 남은 시간 수쿼 문제에서 점수를 더 따 보기로 했습니다. B와 C는 이미 마지막 섭테를 제외하고 모두 긁은 상태에서 진전이 안 되기도 했고...
$l=1, r=N$인 섭테를 어떻게 하면 풀 수 있을까요? 이미 $c_i$가 모두 일정할 때는 풀었지만, 문제는 $c_i$가 일정하지 않은 경우입니다. 앞서 $c_i=cap$으로 고정해 놓고 문제를 풀었는데, 만약 이 $cap$을 $10^{18}$ 정도로 매우 크게 잡으면 어떨까요? 이 경우에도 마찬가지로 함수가 구해지긴 할 것입니다. 차이점이 있다면, $cap$이 매우 크기 때문에 입력 조건에 맞는 어떤 쿼리가 들어와도 $A>B$인 경우는 생기지 않습니다. 즉, 최종 상태가 초기 상태와 완전히 무관해지지 않습니다.
이 사실은 별로 도움이 되지 않아 보입니다. 하지만 여기서 $A, B, C$ 세 변수에 주목할 필요가 있습니다. 이 세 변수가 어떻게 변화하는지, $cap$을 줄이면서 살펴봅시다. $cap$을 1 줄여도 여전히 충분히 크기 때문에 $A>B$일 일은 없습니다. $A$와 $C$는 그대로 있고, $B$는 1 감소합니다. 이러한 현상은 $A>B$가 되기 전까지 계속됩니다.
왜 이러한 현상이 일어날까요? $B$의 한계가 가지는 의미를 보면, $B$라는 값 자체는 큰 의미가 없지만 $cap-B$라는 값은 큰 의미가 있습니다. 사탕 상자 용량의 상한과 초기 사탕의 양 차이가 $cap-B$ 이하로 별로 차이나지 않는다면 용량은 상한에 닿게 되는 것입니다. 따라서 사탕상자의 용량이 $A + (10^{18}-B)$ 이하인 경우 쉽게 해결할 수 있습니다.
사탕상자의 용량이 그보다 작다면 어떨까요? 일단 초기 사탕상자에 담긴 사탕의 양은 더 이상 중요하지 않습니다. (애초에 0이긴 하지만, 100점 풀이에서는 조금 상황이 달라지니 알아는 둡시다.) 따라서 쿼리가 같은 종류일 때, 사탕상자의 용량에 따라 어떻게 최종 상태가 달라지는지를 알 필요가 있겠습니다.
나이브를 통해 여러 가지 관찰을 해 보면, 사탕상자의 용량이 1 증가할 때 최종 상태가 1 증가하거나, 그대로라는 사실을 추측할 수 있습니다. 이것을 그래프로 그리면 기울기가 0인 선분과 1인 선분 여러 개의 합집합이 되는데, 선분의 수도 그리 많지 않아 보입니다. 이제 이를 증명합니다.
쿼리를 나중에 추가되는 것부터 보겠습니다. 마지막 쿼리가 사탕 3개를 추가하는 쿼리라고 가정해 봅시다. 만약 사탕상자의 용량이 3 이하라면, 처음에 사탕이 몇 개였던간에 최종 상태는 무조건 꽉 차있을 것입니다. 반대로 쿼리가 사탕 3개를 제거하는 쿼리였다면, 최종 상태는 무조건 사탕 0개였을 것입니다.
이제 마지막 두 쿼리로 시야를 확장해 봅시다. 만약 마지막 두 쿼리의 $v_i$가 각각 $-5$와 $3$이었다면, 일반적인 경우 사탕 5개를 제거한 뒤 사탕 3개를 추가하므로 사탕 2개가 제거될 것입니다. 하지만 예외가 있습니다.
- 만약 용량이 3 이하라면 최종 상태에서 사탕은 무조건 꽉 차있다.
- 만약 용량이 3 이상 5 이하라면 최종 상태에서 사탕은 무조건 3개이다.
이러한 현상이 왜 일어나는지를 근본적으로 분석할 필요가 있습니다. 일단 현재까지 분석한 바로는, 어떤 쿼리의 $|v_i|$가 용량 $c$보다 크면 최종 상태가 초기 상태에 상관없이 결정됩니다. 그런데 쿼리가 여러 개라면? $v_i$의 부호가 계속 달라져서 $|v_i|$의 합으로는 판단하지 못할 것 같습니다. 그렇다면 $v_i$의 합의 절댓값은 어떨까요?
어떤 사탕상자의 용량이 $c$, 그리고 어떤 쿼리 구간 내에서 $v$의 최대 구간합이 $M$, 최소 구간합이 $m$이라고 해봅시다. $M \ge c$인 경우 이 구간 내에서 사탕상자의 용량은 무조건 상한을 치게 됩니다. 반대로 $m \le -c$인 경우 사탕상자의 용량은 무조건 하한을 치게 됩니다. 이제 목표가 분명히 정해졌습니다. 쿼리를 뒤부터 보면서, 순간적으로 최대 구간 합(또는 최소 구간 합의 절댓값)이 $c$를 넘는 지점을 찾아내면 됩니다.
여기까지 이해했다면 전체 풀이 구상은 어렵지 않을 겁니다. 이 풀이를 $O(N \log N)$ 정도에 구현해서 서브태스크 4를 맞을 수 있습니다.
~ 4시간 48분 (100 67 70)
여기에 서브태스크 3의 루트질을 조합하면 $O((N+Q)\log Q)$에 문제가 풀립니다. 로그를 떼는 것이 조금 까다롭긴 합니다.
~ 5시간 (100 67 70)
이후 C를 더 뚫어보려고 했으나 실패했고, 대회 시간이 그대로 종료되었습니다.
총평
237점이라는 점수는 작년에는 아슬아슬하게 금메달 안에 드는 점수였는데, 올해는 작년보다 문제가 어려웠기 때문에 금메달권에 들지 않을까 기대했습니다. 실제로도 Day 1 성적 7등이 나와서, 예상 이상으로 만족스러운 출발을 했습니다.
Day 2
Day 1에서 비교적 금메달을 받기 안정적인 점수를 받았기 때문에, 이번 대회에서도 어느 정도 안정적인 점수를 받고 나면 욕심을 부려 볼 생각이 있었습니다.
~ 11분 (100 0 0)
이번에도 세 문제를 모두 읽었는데, 1번 문제가 과거 기출과 많이 비슷해 보여서, 그리고 서브태스크 배점이 매우 커서 가장 쉬운 문제일거라고 예상했습니다. 과거 기출문제의 풀이에 누적 합만 더하면 100점 풀이를 매우 쉽게 얻을 수 있었고, 곧바로 코딩해 100점을 받았습니다.
~ 28분 (100 11 0)
B로 넘어갔는데, 자명섭테가 하나도 없어 보여서 당황했습니다. 뭔가 무지성 시뮬레이션으로 풀리는 서브태스크가 하나쯤 있어야 할 문제인데, 잘 보이지 않았기 때문입니다.
그러던 중 1번 서브태스크가 사실 시뮬레이션으로 풀린다는 것을 깨달았습니다. 체력이 모든 던전의 $s_i$보다 커지는 순간 주인공은 모든 경기를 이기게 되고, $N$번 이하의 전투 안에 게임이 끝납니다. 그런데 $s_i$가 모두 10000 이하이므로, 체력은 매 전투 뒤에 증가한다는 가정을 활용하면 $N+10000$번의 전투 안에 항상 게임이 끝남을 알 수 있습니다. 따라서 이걸 그냥 시뮬레이션하면 11점을 받을 수 있습니다.
~ 59분 (100 24 0)
이제 C에서 점수를 긁으려고 했는데, C는 어셈블리 문제였습니다(...) IOI에 어셈블리 문제가 나온 게 물론 처음은 아니지만, 막상 문제를 마주하니 재미있어 보이면서도 당황스러웠습니다. 어쨌든 10분 정도 고민해 봤으나 1번 서브태스크조차 풀 수 없었고, 대회 중만 아니었다면 풀릴 때까지 문제를 잡았겠지만 대회 중이었기 때문에 일단 이성을 되찾고 B에서 점수를 더 얻기로 했습니다.
2번 서브태스크는 배점이 조금 크기도 하고, 어려워 보여서 일단 스킵하고 3번 서브태스크를 생각해 봤습니다. 모든 $s_i$가 같다면 체력이 $s_1$을 넘는 지점이 중요할 것입니다. 그 전까지는 모든 전투에서 지고, 그 후로는 모든 전투에서 이길 것이기 때문입니다. 모든 전투에서 진다고 가정하면, 이 시점을 찾는 것은 스파스 테이블을 이용해 할 수 있습니다. 이 뒤는 $O(N)$ 전처리로 쉽게 풀 수 있고, 따라서 문제가 $O(N \log X + Q \log X)$에 해결됩니다.
~ 1시간 21분 (100 24 21)
이제 진짜 C를 긁어야 할 것 같아서, C를 팠습니다. 두 수 비교부터 쉬운 방법이 떠오르지 않아서 해멨는데, $k \le 2$라는 조건을 이용해서 20번의 연산을 모두 써 가며 풀었습니다.
2비트 이하의 수 중 최솟값은 거의 항상 $x \& y$ 이지만, 딱 한 경우, 두 수가 1과 2일 때 예외입니다. 이 경우만 1이 나오도록 처리가 가능합니다.
~ 1시간 45분 (100 62 21)
2비트 비교로는 어떠한 발전도 할 수 없기 때문에 일단 다시 B로 넘어갔습니다. 4번 서브태스크는 3번 서브태스크에서 스파스 테이블의 수를 5개로 늘리고 귀찮은 처리만 조금 더 해 주면 쉽게 맞을 수 있습니다.
2번 서브태스크는 어떻게 풀어야 할까요? 지는 경우 체력의 변화를 살펴봅시다. 패배했을 때 체력은 처음에 $s_i$ 이하였다가, $s_i$만큼 늘어나므로 체력은 적어도 2배가 됩니다. 그런데 체력이 모든 $s_i$보다 커지면 질 일이 없으므로, 전투에서 패배할 일은 어림잡아 25번 정도밖에 없습니다. 따라서 다음으로 패배할 시점을 적당한 스파스 테이블로 찾아줄 수 있고, 62점 서브태스크를 해결할 수 있습니다.
~ 5시간 (100 62 75)
남은 시간은 대부분 C에 투자하였습니다. 다소 극단적이기도 하지만, B의 89점 풀이의 난이도를 보면 옳은 선택이었던 것 같습니다.
먼저 3번 서브태스크를 봅시다. 이 서브태스크는 10비트의 두 수를 40번 미만의 연산으로 비교하고, 작은 것이 왼쪽에 오게 교환할 수 있으면 풀 수 있습니다. 아래와 같은 메커니즘을 이용합니다. 자잘한 예외 처리는 설명하지 않았습니다.
- 두 수 $x$와 $y$의 XOR을 계산하고, 최상위 비트 이하의 비트를 모두 1로 덮는다.
- 여기에 1을 더하고 2를 나눠 최상위 비트만을 얻어낸다.
- $x$와 최상위 비트의 AND 값을 얻고, $K$개의 비트를 모두 이 비트로 덮는다. (즉 $x$의 최상위 비트가 켜져 있었다면 $2^K-1$, 아니면 0이 얻어진다)
- 이 수와 $x$와 $y$의 XOR을 AND시키고, 이 값을 $x$와 $y$ 모두에 XOR시킨다.
이 메커니즘을 그대로 구현하면 서브태스크 3을 풀 수 있고, 이것을 이용해 버블 소트를 하면 서브태스크 4를 풀 수 있습니다. 마지막으로 이 메커니즘을 병렬로 돌아가게 할 수 있는데, 버블 소트를 병렬로 구현하면 서브태스크 6이 풀립니다.
버블 소트를 병렬로 한다는 것은 아래와 같습니다.
- $n$번의 단계로 $n$개의 수를 정렬하는데, (1-index)
- 홀수 번째 단계는 $f(1, 2), f(3, 4), f(5, 6), \cdots$를 수행하고,
- 짝수 번째 단계는 $f(2, 3), f(4, 5), f(6, 7), \cdots$를 수행한다.
- 단 $f(x, y)$는 $x$번 수와 $y$번 수를 비교해 작은 것을 $x$번 자리에 위치, 큰 것을 $y$번 자리에 위치시키는 조작을 의미한다.
끝나기 10분 전에 만점 풀이를 찾았습니다. 위 교환 메커니즘에서 몇 단계를 효율적으로 수행해 20번 정도의 연산으로 줄일 수 있고, 이를 $\log_2 100$번 정도 수행하면 만점이 나오는데, 시간이 없어서 코딩하지 못하고 대회가 끝났습니다.
총평
Day 2도 Day 1과 똑같은 점수인 237점을 받았습니다. 237점은 300점의 정확히 79%입니다. Day 1보다는 문제가 쉬웠기 때문에 등수가 조금 떨어질 것이라고 예상했지만, Day 1 7등, Day 2 8등으로 종합 성적 7등을 유지했습니다.

제 실력보다 충분히 높은 결과였기 때문에 만족했습니다. 아무래도 욕심을 부리지 않고 초반부터 기본적인 서브태스크를 긁은 것이 좋은 성적을 얻은 요인으로 작용한 것 같습니다. 대회가 끝나고 시간대별로 상황을 정리하며 돌아봤는데, 제가 대회 때 다른 선택을 했더라도 지금보다 좋은 점수를 얻기는 어려웠을 것 같습니다. 또 저에게 익숙한 문제나 익숙한 테크닉을 쓰는 문제가 많이 나와서 운이 좋았던 점도 있던 것 같습니다.
우리나라 성적(1금 2은 1동)이 생각보다 좋지 않았던 점은 아쉬웠습니다. 저보다 잘하는 팀원들이 많았는데, 아마 심적으로 부담감이 크지 않았을까 생각합니다. 앞으로도 최선을 다하겠습니다.
'대회 > 기업 대회 & 올림피아드' 카테고리의 다른 글
| SCPC 2024 Round 2 (D, E) (0) | 2024.07.27 |
|---|---|
| IOI 2022 업솔빙하기 (0) | 2023.02.04 |
| APIO 2021 후기 (1) | 2021.05.27 |
| 폴리매스 제2회 코딩 챔피언십 풀이 및 후기 (4) | 2021.03.03 |
| KOI 2020 고등부 후기 (4) | 2020.11.17 |

