티스토리 뷰
APIO 2021은 작년 APIO보다 많이 어려운 셋이었고, 점수도 받기 힘들었습니다. cms 화면 캡처는 깜박하고 못 했지만, 47+100+36=183점을 획득했습니다. 전체 성적은 29등(은메달) / 한국 1등입니다. 인증샷은 APIO 결과 화면으로 대체합니다.

문제의 난이도가 매우 높았고 구현도 힘들었으며, 대회 중에 채점 큐가 터져서 정말 고난의 연속이었습니다. 물론 그 덕에 시간을 1시간 더 받긴 했고, 결과적으로는 이득이었던 것 같습니다. 아래는 문제별로 제가 생각한 최대 풀이입니다.
A. 육각형 영역
최종 점수: 47점
총평: 100점 풀이는 바로 나왔지만, 구현이 매우 매우 매우 매우 매우 더러워서 시간 내에 도저히 풀 수 없는 문제였습니다. 구현이 간단한 풀이가 있다면 매우 궁금합니다.
서브태스크 1, 2 (9점)
도형이 항상 정삼각형이라는 것을 관찰하면, 나머지는 간단한 수학입니다. 답은 $A \times \frac{(N+1)(N+2)}{2} + B \times (\frac{N(N+1)(2N+1)}{6} + \frac{N(N+1)}{2})$. (여기서 $N$은 정삼각형의 한 변의 길이로, $L[0]$입니다.)
서브태스크 3 (11점)
변의 길이 합이 2000이므로 큰 격자를 만들어 놓고 나이브하게 풀 수 있습니다. 먼저 그림의 육각 격자는 다루기 어려우므로 dual graph를 그려 삼각 격자로 문제를 바꿉니다. 삼각 격자이므로 실제와는 조금 다르게 격자를 만들어야 하는데, 아래 그림처럼 방향별 길이를 설정하면 됩니다. (삼각 격자를 오른쪽으로 2/sqrt(3)배 늘린 것입니다.)
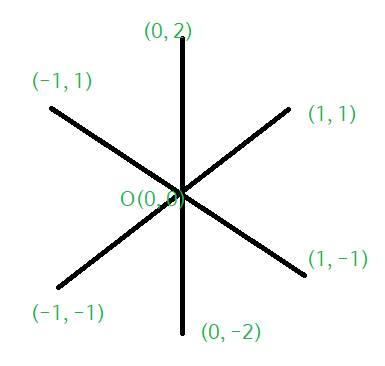
이렇게 하면 격자 위에 다각형의 모든 점을 찍고 바깥쪽을 flood-fill해 안쪽 점들을 구할 수 있게 됩니다. flood-fill을 해준 뒤 bfs를 돌려 각 점까지의 최단 거리를 이용해 답을 계산하면 $O(2000^2)$에 풀립니다.
서브태스크 4, 5 (27점)
위 서브태스크와 같이 좌표계를 모델링하면 삼각 격자가 만들어집니다. $B=0$이므로 점의 개수만 세면 되는데, 기존의 육각형이 dual-graph에서 점이 되었으므로 다각형 경계/내부의 점의 수를 빠르게 세면 됩니다. 이를 연결해 주는 정리로 픽의 정리가 있습니다. 삼각 좌표계에서도 픽의 정리를 사용할 수 있는데, 내부의 점 수는 $I=\frac{A+S}{2} + 1$입니다. 여기서 $A$는 경계 위의 점의 수이고, $S$는 넓이입니다. $A$는 $L$의 모든 원소의 합으로 쉽게 구할 수 있고, $S$는 ccw로 구하면 됩니다. 시간 복잡도는 $O(N)$입니다.
서브태스크 1, 2, 3, 4, 5, 6, 7, 8 (100점) (추정)
사실 이 문제의 100점 풀이로 추정되는 풀이는 대회 시작 10분 안에 얻었습니다. 맞다고 확신할 수는 없지만, 어느 정도 맞는 것 같습니다. 물론 구현에 실패해서 점수를 받진 못했습니다.
문제에서 구해야 하는 것은 결국 각 정점까지의 최단거리의 합입니다. 이것을 쉽게 구할 수 있으면 정점의 개수는 어렵지 않게 구할 수 있을 것이기 때문입니다. 여기서 아래와 같은 관찰이 필요합니다.
Obs. 1) 시작점 $s$에서 어떤 정점 $x$까지 도달하기 위해 지나야 하는 간선을 0 / 180도 방향 간선 (type A), 60 / 240도 방향 간선 (type B), 120 / 300도 방향 간선 (type C)로 구분할 수 있다. 이들의 개수를 $a$, $b$, $c$로 두면, 정점 $x$에 도달하는 모든 최단경로에서 $a+b+c$는 일정하다.
Obs. 2) 사실, $a+b+c$뿐만 아니라, $a$, $b$, $c$ 각각 역시 일정하다. (!)
관찰 1은 자명합니다. 관찰 2에 대한 strict한 증명은 하지 못했지만, 직관적으로 간단하게 이해되는 증명을 소개합니다.
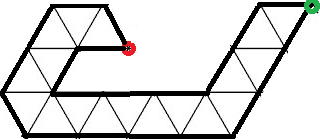
빨간 점이 시작점, 초록색 점이 도착점일 때 빨간 점부터 초록 점까지를 연결하는 곡선을 아무거나 하나 그립니다.

이제 위 곡선을 실처럼 생각하고, 출발점과 도착점 양쪽에서 잡아당기면, 2차원 도형 위에서의 최단경로가 만들어집니다. (단 이 경로는 간선이 아닌 곳을 지날 수도 있기 때문에 우리가 원하는 답은 아닙니다.)
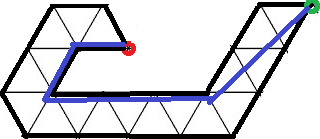
이때 곡선은 선분 유한 개의 집합이 됩니다. 각각의 선분에 대해서 생각해 봅시다. 각각의 선분은 어떤 두 점의 최단 거리 경로입니다. 이때 이 선분의 양끝점을 반대편 꼭짓점으로 갖는 평행사변형을 그릴 수 있습니다. 아래 그림에서 연두색 평행사변형이 이에 해당합니다.
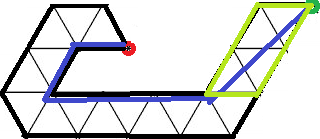
연두색 평행사변형의 서로 반대편 점의 최단거리는 두 가지 방향의 간선만 사용하게 됩니다. 그 이유는 대각선을 막힘 없이 그릴 수 있기 때문에, (위 그림의 경우) 가로 방향 간선과 / 방향 간선만으로 최단 거리로 이동할 수 있기 때문입니다. 따라서 이 평행사변형 내부에서 $a$, $b$, $c$는 어떤 최단경로를 잡든 일정합니다. 따라서 전체 $a$, $b$, $c$도 일정하게 됩니다.
Obs. 3) 모든 0-180 방향 간선의 가중치를 0으로, 나머지 간선의 가중치를 1로 두고 최단경로를 구하면, 그 최단경로의 길이는 $b+c$이다.
Obs. 4) 관찰 3의 알고리즘을 이용해 $b+c$뿐만 아니라 $a+b$, $a+c$를 모두 구해 합한 뒤 2로 나누면, $a+b+c$를 구할 수 있고 이것이 원하는 최단 경로의 길이이다.
따라서 관찰 3에서 모든 정점으로의 최단경로의 길이 합을 빠르게 구할 수 있으면 됩니다. 위 예시 그래프에서 0-180 방향의 모든 간선을 가중치 0으로 둔다는 것은, 해당 방향 간선으로 연결된 모든 정점을 하나로 합쳐 주는 것과 같이 생각할 수 있습니다. 정점을 하나로 합칠 때 정점의 가중치는 그 정점으로 합쳐진 기존 그래프의 정점 수로 둡니다. 그럼 아래와 같은 그래프가 생겨납니다. 이때 정점에 적혀 있는 번호는 정점의 번호이며, 옆에 적혀 있는 수가 가중치입니다.

고정한 방향 간선이 아닌 다른 방향 간선을 통해 한 번에 이동할 수 있는 정점들끼리 묶으면 오른쪽과 같은 트리가 생깁니다. (이 아이디어는 IOI 2012 City의 아이디어와 같습니다.) 트리 자체는 구현이 매우 복잡한 스위핑을 통해 얻어낼 수 있고, 트리 DP를 돌려서 시작점이 포함된 정점에서 다른 점까지의 최단거리 합을 구할 수 있습니다.
아직 한 가지 문제가 남아 있습니다. 위와 같은 방식으로 트리를 만들면 트리의 정점 개수가 $O(L^2)$개 정도까지 커질 수 있기 때문입니다. ($L$은 도형의 둘레) 따라서 이를 해결하기 위해 트리 압축을 사용합니다. 트리 압축의 기본 아이디어는 차수가 2인 정점들을 줄이는 것인데, 위와 같은 모양의 트리에서는 (트리 압축을 적용하게 될) 차수가 2인 인접한 정점의 차수를 보면 가중치가 일정하거나, 1씩 증가하거나, 1씩 감소합니다. 그 이유는 아래와 같은 그림으로 설명됩니다.
Case 1) 양쪽 간선이 평행한 경우

Case 2) 양쪽 간선이 평행하지 않은 경우
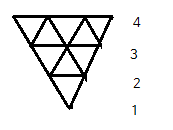
위를 뒤집으면 1 2 3 4와 같이 아래로 갈수록 1씩 늘어나는 패턴이 됩니다.
따라서 트리 압축 뒤 각 간선 위에 $y=ax+b$와 같이 직선을 할당할 수 있고, 이러한 직선을 할당하면 간선 내부 정점들에 대한 답도 트리 DP를 이용해 구할 수 있습니다. 이렇게 하면 트리를 만드는 시간 복잡도 $O(N \log N)$과 트리 DP를 처리하는 시간 $O(N)$, 총 $O(N \log N)$에 문제를 풀 수 있게 됩니다.
B. 밀림 점프
최종 점수: 100점
총평: 전체적으로 어려운 셋에 있는 유일한 (그나마) 쉬어가는 문제. 풀이를 생각하는 것이 까다롭지는 않지만 조금만 잘못 생각하면 사풀로 빠지기 쉬운 문제.
서브태스크 1 (4점)
int minimum_jumps(int A, int B, int C, int D){
return C-B;
}
서브태스크 2, 3, 4 (33점)
$O(NQ)$ 시간에 문제를 풀 수 있기 때문에, 각 쿼리별로 bfs를 돌리면 됩니다. 각 정점별로 왼쪽/오른쪽으로 이동했을 때의 위치를 찾는 것은 스택을 이용해 쉽게 할 수 있습니다.
서브태스크 1, 2, 3, 4, 5, 6, 7 (100점)
먼저, $B$과 $C-1$ 사이의 막대들의 높이 최댓값을 $h$라고 합시다. 이때 $C$나 그 오른쪽에 도달하기 위해서는 높이가 $h$ 이상인 지점에 먼저 도달해야 합니다. (그래야 높이 $h$인 막대를 넘을 수 있습니다.) 따라서 우리는 먼저 높이가 $h$ 이상인 지점에 도달해야 합니다.
만약 $C$에서 $D$ 사이로 이동하는 것이 가능하다면, 높이가 $h$ 이상인 지점에서 단 한 번만 오른쪽으로 이동해도 목적지에 도달하는 것이 가능합니다. 하지만 만약 높이가 $m$ 이상인 지점(단, $m$은 $C$에서 $D$ 사이의 높이 최댓값)에 도달해 버리면, 더 이상 $C$와 $D$ 사이의 점으로 이동할 수 없게 됩니다. 따라서 높이가 $h$ 이상 $m$ 미만인 지점에 도달하기 위한 최소 이동 횟수를 찾으면 됩니다.
먼저 논리를 편하게 전개하기 위해 이동이 불가능한 경우부터 걸러냅시다. 이동이 불가능한 경우는 생각보다 단순한데, $B$에서 오른쪽으로만 이동했을 때 $C$와 $D$ 사이의 점을 한 번도 지나지 않는 경우입니다. 이것을 구하는 방법은 다음과 같습니다. 먼저 각 점 $x$에서 $2^i$번 오른쪽으로 이동했을 때 도달하는 위치를 스파스 테이블로 관리합니다. 그리고 스파스 테이블에서 이분 탐색을 하는 기법을 이용해 점 $x$에서 도달할 수 있는 $D$ 이하의 점 중 가장 오른쪽에 있는 점을 구합니다. 이 점이 $C$ 이상의 위치에 있으면 이동할 수 있는 것이고, $C$ 미만이면 이동할 수 없으므로 반복문을 바로 빠져나올 수 있습니다.
만약 도달이 가능하다면, 우선 어떤 점에서 시작할지를 결정해 봅시다. 시작점으로 의미가 있는 점은 아래에서 빨간색 위치들과 같은 형태라는 관찰을 할 수 있습니다. 초록색 위치들의 경우 $B$보다 오른쪽에 도달하려면 자기 오른쪽에 있는 빨간 선분을 하나라도 넘어야 하는데, 이럴 바에는 빨간 선에서 시작하는 것이 유리하기 때문입니다. 따라서 가능한 출발지는 $B$에서 시작해 왼쪽으로 이동하면서 만나는 $A$와 $B$ 사이의 위치들이라고 생각할 수 있습니다. 이들 중 $h$ 이상 $m$ 미만의 높이를 가진 점이 있다면 단 한 턴에 이동이 가능할 것입니다. 하지만 그런 점이 없다면, 높이가 $m$ 이하인 점 중 가장 높은 점으로 가는 것이 최적입니다. 이것은 앞에서 말한 스파스 테이블을 반대 방향으로 관리하여 구할 수 있습니다.

만약 시작점의 높이가 $h$ 이상이라면 앞서 언급했듯이 쉽게 끝낼 수 있습니다. 문제는 시작점의 높이가 $h$ 미만인 경우인데, 이 경우 최대한 빠르게 높이가 $h$ 이상 $m$ 이하인 지점으로 이동해야 합니다. 여기서 하나의 sparse table을 더 관리합니다. 이번에는 왼쪽이나 오른쪽과 같이 방향을 정한 것이 아닌, 그때 그때 이동할 수 있는 왼쪽과 오른쪽 방향 점 중 더 높은 곳으로 이동하는 스파스 테이블입니다. 이제 이분 탐색을 하여 높이가 $h$ 미만인 (갈 수 있는) 가장 높은 점으로 이동합니다. 여기서 $h$ 이상 $m$ 미만로 한 번의 이동에 갈 수 있다면 바로 알고리즘을 종료할 수 있고, $h$ 이상으로 갈 수 있는 모든 후보가 $m$ 이상이라면 여기서부터는 오른쪽으로만 이동해서 목표에 도달해야 할 텐데 이 역시 스파스 테이블로 구할 수 있습니다.
앞서 언급한 세 개의 스파스 테이블을 전처리해 두고 이분 탐색으로 답을 빠르게 찾으면 총 시간 $O((N+Q) \log N)$에 문제를 풀 수 있습니다.
C. 도로 폐쇄
최종 점수: 36점
총평: 전형적인 small-to-large 트리DP 문제. 하지만 이런 유형을 많이 풀어보지 않아서 어려웠던 문제.
서브태스크 1, 2 (12점)
각각 정렬 / DP로 풀립니다. 풀이는 생략합니다.
서브태스크 3, 4 (24점)
다음과 같은 DP를 생각할 수 있습니다.
$DP[i][j]$: $i$번 노드의 서브트리 이하의 정점을 모두 차수가 $j$ 이하로 만들기 위해 $i$의 서브트리 위의 간선이나 $i$와 부모와의 간선을 적절히 자를 때 필요한 최소 비용
$DP2[i][j]$: $DP[i][j]$와 같으나, 정점 $i$와 부모와의 간선을 반드시 잘라야 할 때의 최소 비용
$i$의 자식 노드의 집합을 $S_i$라고 합시다. 이때 $DP2[i][j]$를 구하려면 정점 $i$의 부모와의 간선을 반드시 자르고, 자식 노드 중에 간선을 자를 것을 선택할 수 있습니다. 자를 것이면 그 자식의 $DP2[c][j]$ 값을, 자르지 않을 것이면 그 자식의 $DP[c][j]$ 값을 취할 수 있습니다. 그런데 차수가 $j$ 이하여야 한다는 조건 때문에 최소 몇 개 이상의 간선은 잘라야 하고, 따라서 $DP[c][j]$를 최대 $l$개만큼 고를 수 있습니다. ($l$은 간단한 사칙연산으로 구해집니다.)
이때 $DP[c][j]$를 최적으로 구하기 위해서는 IOI 2020 Day 1: Tickets 와 동일한 트릭을 쓸 수 있습니다. 먼저 $DP2[c][j]$의 전체 합을 구해 두고, $DP[c][j] - DP2[c][j]$의 값을 정렬하여 양수인 것 중 상위 $l$개 ($l$개 이하라면 전체의 합)을 구해 줘서 더하면 됩니다. 이렇게 하면 $DP2[i][j]$가 구해집니다. $DP[i][j]$도 같은 방식으로 구할 수 있습니다. 이때 시간 복잡도는 $O(N^2 \log N)$입니다.
100점 풀이는 다른 참가자 분들의 블로그를 참조하시면 되겠습니다.
'대회 > 기업 대회 & 올림피아드' 카테고리의 다른 글
| IOI 2022 업솔빙하기 (0) | 2023.02.04 |
|---|---|
| IOI 2021 후기 (14) | 2021.06.28 |
| 폴리매스 제2회 코딩 챔피언십 풀이 및 후기 (4) | 2021.03.03 |
| KOI 2020 고등부 후기 (4) | 2020.11.17 |
| NYPC 2020 예선 풀이 (5) | 2020.09.06 |

