티스토리 뷰
Problem Solving Diary #16 - ICPC Seoul Regional 2021
79brue 2024. 1. 20. 22:54이제 곧 ICPC에 참가해야 하기 때문에 ICPC 입문을 조금 해 보기로 했다. 입문 셋으로 ICPC Seoul Regional 2022를 골랐다. 시간은 딱히 재지 않고 문제를 쉬운 것부터 풀어보았다.
J. Parentheses Tree
입력으로 주어지는 괄호 문자열을 파싱하는 문제이다. 스택으로 트리를 만들고 DFS를 돌리는 방법도 있지만 시간이 오래 걸릴 수 있다. 트리를 만드는 과정에서 깊이를 관리하면 상수가 더 작고, 따로 스택을 관리할 필요도 없다(실제 트리의 구조를 만들지 않아도 되므로). 시간 복잡도는 $O(|S|)$이다.
F. Frog Jump
KOI 2019 중등부 2번 문제에 비슷한 게 있었던 것 같다.
서로 겹치는 구간들의 번호가 인접하기 때문에, 이들을 그룹으로 묶어 준다. 이렇게 묶인 구간을 왼쪽부터 보면서, 인접한 그룹 사이의 점프 거리를 구해 준 뒤 그 누적합을 구해 주자. 이후에 점프를 할 때는 누적합을 이용해 점프 거리 합을 계산하면 된다. 시간 복잡도는 $O(N+K)$이다.
I. Palindrome Type
어떤 문자열에서 0, 1, 2, 3개의 문자를 제거해 팰린드롬을 만들 수 있는지 확인해야 한다.
양쪽에서부터 같은 문자를 한 개씩 제거하되, 왼쪽 또는 오른쪽 문자 중 하나를 건너뛸 수 있는 skip을 최대 3번 할 수 있다고 생각하자. $(l, r)$을 정점으로 보고 그래프에서 최단거리를 구한다고 생각할 수 있다. 이때 skip이 3번밖에 없기 때문에 가능한 정점의 수가 $O(N)$이고, 다익스트라 알고리즘으로 문제를 풀 수 있다. 시간 복잡도는 $O(n)$이다. (0-1 BFS도 될 것 같다)
K. Shuffle Game
$DP[i][j][k]$가 카드 덱의 $i$번째 카드까지와 $P_1$의 $j$번째 카드까지, 그리고 $P_2$의 $k$번째 카드까지만을 보았을 때 가능한 최대 답이라고 하자. $DP[i][j][k]$는 $DP[i-1][j][k]$, $DP[i][j-1][k]$, $DP[i][j][k-1]$, $DP[i-1][j-1][k]$, $DP[i-1][j][k-1]$의 다섯 가지 항으로 점화식을 세울 수 있다. 이때 시간복잡도는 $O(npq)=O(n^3)$이다.
E. Forbidden Turns
다익스트라를 돌리되, 정점으로 방문 체크를 하지 말고 간선으로 방문 체크를 하면 된다. outdegree가 10 이하라는 조건이 있어서 이렇게만 처리해도 $O(10 m \log m )$에 해결할 수 있다.
D. Folding Stick
문제 해석이 좀 걸렸는데, 수열을 구간으로 나눠 각 구간에 있는 수들의 합을 $S_1, \cdots, S_k$라 할 때, $S_1 \le S_2 \cdots \le S_{k-1}$을 만족해야 한다. ($S_k$는 $S_{k-1}$보다 작아도 됨) 이때 $\max S_i$를 최소화하는 문제이다.
$DP[i]$를 $i$번 선분이 한 구간의 끝 선분일 때 현재까지의 $\max S_i$라고 정의하자. 이때 두 가지 option이 있다.
- $i+1$번부터 $n$번까지 선분이 전부 마지막 구간을 이룸: 이때는 누적합을 이용해 답을 갱신해준다. $sum[i]$를 $1$번부터 $i$번까지 선분 길이 합이라고 하자. 이때 답에 $\max(DP[i], S_n - S_i)$를 후보 중 하나로 갱신할 수 있다.
- $i+1$번 선분이 마지막 구간에 포함되지 않음 -> $S_i$의 증가 조건에 의해 구간의 끝 선분 번호 $j$의 최솟값이 존재한다. 이를 이분 탐색으로 찾는다. $j\le idx$인 $idx$에 대해 $DP[idx]$를 $S_{idx} - S_i$로 갱신해 주는 것이 가능하다. $here[i]$라는 배열을 만들어 $here[idx]$를 $\max(here[idx], S_i)$로 갱신하자. 이렇게 하면 $DP[i]$를 갱신하는 것을 $S_i - \max_{j \le i} here[j]$로 하는 것이 가능하다.
따라서 문제를 $O(n \log n)$에 해결할 수 있다.
L. Two Choreographies
정점 수 $n$의 무방향 그래프 $G$는 정확히 $2n-3$개의 간선이 있다. 두 회로 $A$와 $B$를 만들되, 그 길이는 $l \ge 3$으로 같아야 하고, $A$에만 등장하고 $B$에는 등장하지 않는 간선 $e_A$와 $B$에만 등장하고 $A$에는 등장하지 않는 간선 $e_B$가 모두 존재해야 한다.
$G$의 임의의 스패닝 트리 $T$를 잡자. $G=(V, E)$일 때 $E-T$의 집합 (트리에 포함되지 않은 간선의 집합)을 $F$라고 하자. $\forall e \in F$에 대해 $e={x, y}$라고 한다면 $x$와 $y$의 거리를 $dist(e)$라고 하자. $2 \le dist(e) \le n-1$을 만족한다. $|F|=n-2$이므로 이론적으로는 $dist(e)$가 모두 다를 수 있다.
그러나 만약 $T$가 일직선 형태의 트리가 아니라면, $2 \le dist(e) \le n-2$이므로 비둘기집의 원리에 의해 적어도 한 쌍의 $(e_1, e_2)$가 존재해 $dist(e_1) = dist(e_2)$이다. 따라서 $G$에서 일직선 형태가 아닌 서브트리를 하나 잡고, $dist$가 같은 트리 밖의 간선 두 개를 골라 회로를 구성하면 문제를 풀 수 있다.
연결 성분이 여러 개인 경우에 조심해서 문제를 풀면, $O(n)$에 문제를 해결할 수 있다.
C. Empty Quadrilaterals
티어상으로는 A가 더 쉽긴 한데 딱 보고 이건 아니다 싶어서 C로 도망쳤다.
사각형의 한 대각선을 고정하고, 이 대각선의 양끝점을 $A$와 $C$라고 하자. $AC$ 양쪽에서 점 $B$와 $D$를 찾아야 하는데, 일단 $B$로 가능한 점들과 $D$로 가능한 점들의 후보를 구해야 한다. $B$를 고르는 가짓수를 구하기 위해서는, 편의상 아래 위치 관계를 생각하자.
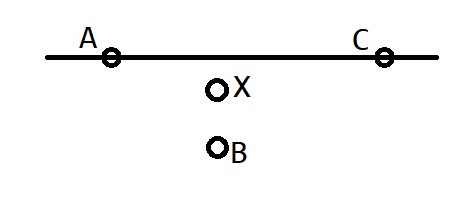
$AC$ 아래에 있는 점들의 집합을 $S$라고 하자. $S$의 점들을 $A$에서의 각도를 기준으로 시계 반대 방향으로 1부터 번호를 붙이고, 마찬가지로 $C$에서의 각도를 기준으로 시계 반대 방향으로 1부터 번호를 붙이다. 이때 점 $B$가 번호 $(a_1, c_1)$을 받았고, $X$가 번호 $(a_2, c_2)$를 받았다면, $\triangle ABC$에 $X$가 포함될 조건은 $a_1 < a_2$, $c_1 > c_2$이다.
이것을 좌표평면에 찍어 보면 $N$개의 점 중 $x$가 더 크고 $y$가 더 작은 점이 없는 점의 개수를 세는 것과 같다. 이것은 $a$값과 $c$값을 모두 구해 두고 인덱스들을 정렬하면 선형에 쉽게 해결할 수 있는 문제이다.
이론적으로는 위 과정의 $B$와 $D$를 모두 연결해 사각형을 만들 수 있으므로 그냥 두 경우의 수를 곱하면 될 것 같다. 그러나 문제는 볼록다각형은 두 번 세지는 반면 오목다각형은 한 번 세어진다는 것이다. 이를 해결하기 위해서는 추가적인 처리를 해 주어 오목다각형일 때 두 번 세어지도록 해야 한다. $\square ABCD$가 오목다각형일 조건은 $BD$가 $AC$ 기준으로 $A$의 왼쪽에 있거나 $C$의 오른쪽에 있는 경우이다. 두 경우는 동시에 일어나지 않으므로 각각을 세어 주면 충분하다. $BD$가 $A$의 왼쪽을 지나갈 조건은 $ccw(B, A, D) > 0$이다. 이것은 정점들을 $A$ 기준에서 본 각도순으로 양쪽 반평면에서 따로따로 정렬해 놓고 two pointer 등을 쓰면 셀 수 있다.
이렇게 문제를 해결하면 시간 복잡도가 $O(n^3 \log n)$인데, 시간 초과가 난다. 전처리를 적절히 해서 $O(n^3)$으로 줄일 수 있다. 구현을 제대로 생각해놓지 않고 짜면 매우 까다롭다. 나는 $O(n^3 \log n)$ 코드를 짠 뒤 시간초과가 나서 로그가 붙은 부분 중 일부 부분만 $O(n^3)$으로 고쳐 맞았다.
A. Card Game
BOJ 16883과 같은 문제라고 한다. 한 시간 고민했는데 풀이를 모르겠어서 태그를 깠다. 스프라그 그런디 정리가 뭔지 몰라서 처음으로 공부했다.
$N, M \le 25$라는 애매한 제한이 바로 눈에 들어오는 문제다. 먼저 게임판을 체스판처럼 색칠하고 검은 칸 / 하얀 칸을 따로 생각하자.
먼저 검은 칸에만 집중해 보자. 한 대각선이 지워지면 게임판은 둘로 쪼개지며, 양쪽 게임판은 서로에게 영향을 주지 못한다. 이런 아이디어에서 착안해 구간 병합 DP와 비슷한 접근을 시도해 볼 수 있다. 편의상 게임판을 45도 돌려 가로/세로 방향으로 카드가 제거되는 것으로 생각하자. 이때 가로와 세로 길이는 모두 $\max(N, M)$ 이하이다. 여기서 분리된 게임판은 $(x_l, x_r, y_l, y_r)$의 상태로 표현할 수 있다. 이렇게 하면 $O(N^4 )$ 개 정도의 복잡도로 모든 상태를 나타낼 수 있다.
이제 스프라그 그런디 정리를 안다면, $O(N^6)$에 쉽게 문제를 해결할 수 있을 것이다. 꽤 큰 시간 복잡도 같지만 상수가 $\frac{1}{36}$ 정도로 매우 작기 때문에 문제를 풀 수 있다.
H. Longest Substring
Suffix Tree에서 sqrt decomposition 비슷한 무언가를 통해 문제를 두 개의 파트로 나눠서 푸는 풀이를 구상하고, 이 풀이라면 문제를 절대 대회에 낼 것 같지 않다고 생각해 풀이를 읽었다. 신기했다.
B. Castle Design
먼저 문제의 문자열이 1-monotone인지 2-monotone인지 구별하자. 다음과 2-monotone성이 동치임을 증명할 수 있다.
- 문자열을 원형으로 나열했을 때, LL이 총 4번 등장한다.
위 사실을 엄밀하게 증명하는 것은 조금 어려워 보인다. 성을 좌표평면으로 나타내고, 각 $x$에 대해 성 내부에 있는 y좌표 구간을 $[l_x, r_x]$로 나타낸 뒤 $l_x$가 최댓값을 기준으로 양쪽으로 감소하는 형태임을 보이고, $r_x$는 최솟값을 기준으로 양쪽으로 증가하는 형태임을 보이는 것이 증명의 시작이 될 것이다. 그러나 엄밀하게 증명하지 않아도 직관적으로 이해할 수 있는 부분이 많으므로 넘어가기로 하자.
이제 $t=1$인 경우와 $t=2$인 경우를 독립적으로 해결한다. $t=1$일 때 $N \le 10^4$, $t=2$일 때 $N \le 10^5$로 제한이 상이함에 조심하자.
$t=2$
이 경우 LL의 등장 위치에 따라 각 사분면 위치에서 R이 등장하는 횟수를 시계 반대 방향으로 $a$, $b$, $c$, $d$라 하자. 예를 들어, 아래 예시에서 1사분면 부분은 R이 한 번 등장하고 $a=1$이다. 마찬가지로 2사분면에서 $b=2$, 3사분면에서 $c=1$, 4사분면에서 $d=1$이다.

이런 형태의 도형에서 rectilinear polygon의 둘레는 해당 polygon을 둘러싸는 직사각형과 둘레가 같음에 주목하자. 이때 가로 길이는 $\max(a+b+1, c+d+1)$ 이상이어야 하고, 세로 길이는 $\max(a+d+1, b+c+1)$ 이상이어야 함을 알 수 있다. 그렇다면 이것이 항상 최소일까? WLOG $a \ge b, c, d$라고 생각하자. 이 경우를 관찰해 보면 $a = c$, $b=d=0$인 경우를 제외하고는 항상 위 최솟값이 성립함을 관찰할 수 있다. 예외로 $a=c$, $b=d=0$인 경우에만 답이 $4a+6$임을 알 수 있다.
$t=1$
$t=1$인 rectlinear polygon의 둘레에 대해서 자세히 생각해 보자. 도형을 돌린다고 해서 turn sequence가 변하지 않으므로 편의상 1-monotone rectlinear polygon은 y축에 평행한 모든 선에 대해 다각형과의 교점이 $0$, $2$, $\infty$개 중 하나라고 정의한다. 이러한 도형은 경계를 "위쪽 경계"와 "아래쪽 경계"로 나눌 수 있다. 아래 그림에서 빨간색 부분을 위쪽 경계, 초록색 부분을 아래쪽 경계라고 부르자.
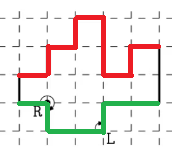
모든 L 또는 R은 위쪽 경계 또는 아래쪽 경계 중 정확히 하나에 속한다는 것을 알 수 있다. 그리고 두 경계를 나누는 기준은 입력으로 주어지는 원형 문자열에서 적당한 구간이 될 것이라는 사실도 알 수 있다. 이를 통해 위쪽 경계와 아래쪽 경계로 가능한 경우의 수가 최대 $O(N^2)$가지임을 관찰할 수 있다.
모든 $O(N^2)$가지 경우가 다 되는 것이 아니다. 아래쪽 경계에 대해, 해당 경계의 문자열이 만족해야 하는 조건을 찾아보자. 일단 첫 문자와 마지막 문자는 모두 $L$이어야 함이 자명하고, 이는 위쪽 경계에도 적용되는 사항이다. 따라서 위쪽 경계와 아래쪽 경계 모두 $L \dots L$ 형태의 문자열일 것이다. 추가로 $L$을 $+1$, $R$을 $-1$로 놓고 누적합을 구해 배열을 만들면, 다음 성질이 모두 성립해야 한다.
- 누적합의 마지막 원소는 $2$여야 한다. (이는 전체 문자열에서 $L$이 $R$보다 두 번 더 나와야 한다는 사실을 의미한다)
- 누적합은 항상 최소 $0$ 이상이어야 하며, 최대 $2$ 이하여야 한다.
여기서 알 수 있는 사실은, 입력이 항상 1-monotone rectlinear polygon이라고 가정하면 위 조건을 만족하는 위경계/아래경계 분할이 항상 존재한다는 것이다. 위와 같은 방식으로 전체 문자열에서 누적 합을 구했다고 해 보자. 이때 위에서 찾은 성질을 생각한다면 누적합 그래프는 다음과 같은 형태일 것이다.

위 그림을 보면 위쪽 경계와 아래쪽 경계로 가능한 경우의 수가 극히 적을 것임을 짐작할 수 있다. 전체 누적 합에서 가장 작은 값과 큰 값의 차이는 $6$를 넘을 수 없다. 위쪽 경계 구간과 아래쪽 경계 구간 중 $S$를 일직선 문자열로 해석했을 때 끊어지지 않고 연결된 것이 최소 하나 있을 것인데, 그것은 누적합의 시작과 끝이 정확히 $2$ 차이날 것이다. 해당 구간의 누적합이 $a$에서 시작해 $a+2$에서 끝난다고 해 보자. 모든 가능한 입력에서 $a=0$, $a=1$, 또는 $a=2$ 셋 중 하나로 잡을 수 있음을 알 수 있다. $a$를 정하면 $a$ 왼쪽의 누적합은 모두 $a$ 이하여야 하고, $a+2$ 오른쪽의 누적합은 모두 $a+2$ 이하여야 하는데, 이 조건을 만족하지 않는다면 해당 $a$는 불가능한 $a$라는 것을 알 수 있다.
이제 $a$가 정해진 경우를 생각하자. 이것은 우리가 위쪽 경계와 아래쪽 경계를 구분할 수 있게 되었다는 뜻이다.
이제 문제를 해결하기 위해 DP를 생각해 볼 수 있다. 편의상 왼쪽 경계 (위쪽 경계와 아래쪽 경계를 연결하는 두 선분 중, x좌표가 더 작은 것)을 $x=0$에 두고, 해당 선분의 끝점을 각각 $(0, 0)$과 $(0, k)$에 두는 경우를 생각해 보자. $DP[i][j][k]$는 위쪽 경계의 $i$번째 세로 선분까지 처리하였고 아래쪽 경계의 $j$번 세로 선분까지 처리하였을 때, 양쪽의 가로 선분 $y$좌표 차이가 $k$라면, 현재까지 이용한 최소 둘레라고 정의하자. 이렇게 하면 전이하는 데 $O(N)$ 정도가 걸려 $O(N^4)$ 풀이가 나온다.
물론 문제를 푸는 데 이 정도 풀이로는 어림도 없고, 시간 복잡도를 줄여야 한다. 먼저 전이를 빠르게 하는 것을 고민해 보자. 가능한 전이를 자세히 설명하면 다음과 같다.
- 위쪽 경계에서 위로 올라간다.
- 아래쪽 경계에서 아래로 내려간다.
- 위쪽 경계에서 아래로 내려간다.
- 아래쪽 경계에서 위로 올라온다.
특히, 위쪽 경계와 아래쪽 경계를 동시에 움직일 수도 있음에 주의해야 한다. 이때 위쪽 경계를 $k$ 이상 아래로 내리는 것은 불가능하며, 마찬가지로 아래쪽 경계를 $k$ 이상 위로 올리는 것도 불가능하다. 마지막으로 위쪽 경계와 아래쪽 경계 사이를 좁히는 경우 그 합이 $k$ 미만이어야 한다.
그러나 이런 식으로 문제를 해결하면 어려움이 많다. 여러 케이스에 대해 관찰해보면 위쪽 경계와 아래쪽 경계 중 큰 것이 좌우 너비가 된다는 사실을 추측할 수 있다. 따라서 더 작은 쪽을 큰 쪽과 겹치지 않게 끼워 넣는 문제가 된다. 일단 맨 왼쪽 경계와 오른쪽 경계를 가능한 최솟값으로 두고, 필요에 따라 늘리는 전략을 선택해 보자. 이때 만약 상하 선분의 길이를 늘릴 일이 있다면 무조건 이 왼쪽/오른쪽 경계를 늘리는 것이 최선임을 알 수 있다. 그렇다면 중앙 둘레는 변하지 않고, 왼쪽/오른쪽 경계를 얼마까지 늘려야 가능한 해가 생기는지를 묻는 문제가 된다. 따라서 일단 좌우경계를 늘리지 않고 진행했다고 가정한 뒤에, DP를 진행하면서 그 늘리는 값의 최솟값을 갱신해 나가면 된다. 정확히는, $DP[i][j]$는 위쪽 경계에서 $i$번 세로줄까지, 아래쪽 경계에서 $j$번 세로줄까지 처리했을 때 위/아래 경계의 간격을 넓혀야 하는 최소의 길이로 정의하면 $O(N^2)$에 문제를 해결할 수 있다.
BOJ 26108. Linear Regression
티어를 보고 바로 포기했다.
'시리즈 > Problem Solving Diary' 카테고리의 다른 글
| Problem Solving Diary #18 (0) | 2024.04.06 |
|---|---|
| Problem Solving Diary #17 (0) | 2024.03.17 |
| Problem Solving Diary #15 (3) | 2024.01.05 |
| Problem Solving Diary #14 (0) | 2024.01.02 |
| Problem Solving Diary #13 (0) | 2023.01.20 |
